머신러닝 기초 - 편미분(Partial Derivative) 이란?

Partial Derivative 는 주로 여러 변수가 있는 함수를 대항으로 미분할 때 사용된다.

편미분을 사용해야하는 경우. x또는 y의 기울기 대해서 미분을 적용할 수 있다.

예를 들어, 위와 같은 표면이 있다고 할 때,

1. x 에 대해서 기울기를 구할 수 있고(y는 고정된 상태)

2. y에 대해서 기울기를 구할 수도 있다(x는 고정된 상태)

위의 그림을 함수로 표현해 보면 다음과 같다.

f(x, y) = x^2 + y^3

x에 대해서 기울기를 구하면 power rule 에 의해 f'(x) = 2x가 된다. 이 경우에서, y^3는 상수로 취급된다

y에 대해서 기울기를 구하면 power rule에 의해 f'(y) = 3y^2가 된다. 이 경우에서 x^2는 상수로 취급된다

실생활의 예제에서는, 실린더의 voume를 구하는데에 사용될 수 있다.

 

편미분은 실린더의 부피 변화를 계산하기 위해서 사용된다

위와 같은 실린더에서, 실린더는 다양한 변수 값을 갖는다.

함수로 나타내면 다음과 같다.

f(r, h) = π r2 h

반지름에 대해서 편미분을 적용하면, f’r = π (2r) h = 2πrh 이 된다.

높이에 대해서 편미분을 적용하면 f’h=πr2(1)=πr2 이 된다.

우리는 미분한 식에서 반지름 혹은 높이 증가에 따라 부피가 얼마나 증가하는지를 구할 수 있다. 

 

편미분은 Chain rule에서도 적용될 수 있다.

y = f(u), u = g(x) 와 같은 식에서, y에 대해서 x를 미분해 보자.

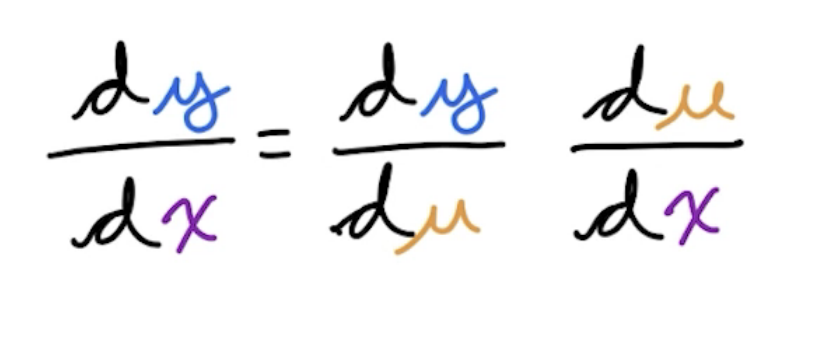
Chain rule를 적용했다

Chain rule에 의해서 위와 같이 미분이 가능하다. 그렇다면 변수가 여럿이라면 어떨까?

 

y = f(u), u = g(x,z) 와 같은 식에서 y에 대해서 x와 z를 미분해 보자.

위와 같이 나타낼 수 있다. 관계도를 그리면 계산이 편해진다.

일반화하면 다음과 같다.